Questa pagina raccoglie alcuni cenni sulle trasformazioni termodinamiche dei gas. Premetto che la mia esposizione non può che essere di parte, essendo chimico, e quindi chiedo scusa in anticipo per eventuali imprecisioni o sviste.

Assicuratevi di aver letto le basi presso Termodinamica I per comprendere i contenuti di questa pagina. Vi è in programma un restyling per rendere questa molto più precisa senza perdere in chiarezza ed immediatezza. Continuate a seguire di tanto in tanto per i nuovi aggiornamenti.

Qui di seguito trovate una tabella riassuntiva con tutti i dati e le formule: Trasformazioni dei gas

- volume
- pressione
- temperatura
- massa

Esiste un'equazione, cioè l'equazione di stato dei gas perfetti, che ci consente in modo approssimativo di calcolare tutte le grandezze di stato del gas. Questa dice:

pV = nRT

con p la pressione in pascal, V il volume in m³, n il numero di moli, R la costante dei gas (8,314472 J/mol*K), T la temperatura in kelvin.

- - - - -

La trasformazione definita ISOCORA avviene quando il volume rimane costante:

Ricaviamo dunque dall'equazione dei gas perfetti che, siccome n, R e V rimangono costanti,

p/T = cost [seconda legge di Gay-Lussac]

cioè il rapporto tra la pressione e la temperatura rimane costante.

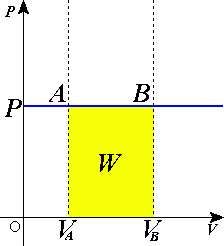
Il lavoro di questa trasformazione è 0 (perché l'area della figura che risulta proiettando verso l'asse delle ascisse il grafico è di superficie nulla), la quantità di calore [per il primo principio della termodinamica] è uguale alla variazione dell'energia interna, che si calcola così:

Q = ΔU = nc_vΔT

con Q quantità di calore, ΔU variazione dell'energia interna, c_v calore molare a volume costante, ΔT variazione della temperatura.

- - - - -

La trasformazione ISOBARA avviene a pressione costante:

Dall'equazione dei gas perfetti troviamo che:

V/T = cost [prima legge di Gay-Lussac]

il rapporto fra volume e temperatura (sempre in metri cubi e gradi kelvin) rimane costante.

Il lavoro di questa trasformazione (identificato dal colore giallo) corrisponde all'area del quadrilatero di base (V_finale - V_iniziale) ed altezza p (come un qualunque rettangolo), oppure, in formula:

L = pΔV

e, per quanto riguarda calore e variazione dell'energia interna:

ΔU = nc_vΔT [come nella trasformazione isocora]

Q = ΔU + L [primo principio della termodinamica] => pΔV + nc_vΔT [dalle eq. precedenti] => nc_pΔT

con c_p il calore molare a pressione costante. Ricordiamo che c_v e c_p sono propri di ogni gas. Il loro rapporto c_p/c_v ci dà γ [gamma]. c_p è sempre più grande di c_v perché c_p = c_v + R, e di conseguenza gamma è sempre maggiore di 1.

Ecco una convincente rappresentazione di una trasformazione a pressione costante:

- - - - -

La trasformazione ISOTERMA avviene a temperatura costante:

Sempre dall'eq. di stato dei gas perfetti ricaviamo

pV = cost [legge di Boyle]

pressione e volume sono inversamente proporzionali: sul piano di Clapeyron la trasformazione isoterma è rappresentata da un ramo di iperbole equilatera.

Partendo dal primo principio della termodinamica, che rimane sempre

Q = ΔU + L

avremo questa volta ΔU = 0 in quanto la temperatura non cambia, e perciò Q = L. Sappiamo comunque che

L = nRT ln(V_finale / V_iniziale)

con ln(V_f / V_i) il logaritmo naturale del rapporto fra volume finale e volume iniziale. n, R e T non variano. Ricordiamo che nel caso ci manchino dati come n o T, possiamo sfruttare sempre l'equazione dei gas perfetti per ricavare uno dei volumi: L = p_aV_a ln(V_b / V_a) oppure L = p_bV_b ln(V_b / V_a), a seconda dei dati. Attenzione per le formule inverse.

Ecco una convincente rappresentazione di una trasformazione a temperatura costante:

- - - - -

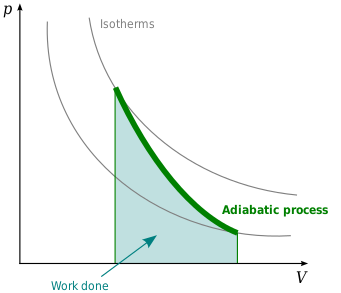
Una trasformazione si definisce ADIABATICA quando il gas non scambia calore con l'esterno ( Q = 0 ). Ciò non significa che la temperatura rimane la stessa: calore è sinonimo di energia, vuol dire che la somma fra il lavoro compiuto dal gas, con la sua variazione di temperatura, compensa la variazione di energia interna. In formula:

L = - ΔU

- Se il lavoro è positivo, il gas compie un lavoro verso l'esterno -> ΔU negativo -> la temperatura diminuisce
- Se il lavoro è negativo, il gas riceve un lavoro dall'esterno -> ΔU positivo -> la temperatura aumenta

Rappresentata graficamente, un'adiabatica ha una curva più ripida dell'iperbole dell'isoterma. Notiamo ancora il lavoro che corrisponde alla superficie individuata dalla proiezione della curva della trasformazione sull'asse dell'ascisse, indicata dal colore verde.

Abbiamo tre formule per ricavare le grandezze di stato, utilizzando il sopracitato valore gamma (come esponente):

1) pV^γ = cost
2) TV^γ-1 = cost
3) Tp^(1-γ)/γ = cost

La prima: pressione per volume alla gamma uguale costante, la seconda: temperatura per volume alla gamma meno uno uguale costante, la terza: temperatura per pressione alla uno meno gamma fratto gamma uguale costante. Particolare attenzione a ricavare le grandezze con le formule inverse:

dalla prima: p_A = p_B (V_B / V_A)^γ oppure V_A = V_B (p_B / p_A)^1/γ (scambiate le lettere per ottenere i dati omologhi)
dalla seconda: T_A = T_B (V_B / V_A)^γ-1 oppure V_A = V_B (p_B / p_A)^1/(γ-1)
dalla terza: T_A = T_B (p_B / p_A)^(1-γ)/γ oppure p_A = p_B (T_B / T_A)^γ/(1-γ)

Ecco alcuni dati interessanti da usare nei problemi:

R = 8,314472 J/(mol K)

se il gas è monoatomico (esempio: argon [Ar]):
c_v = (3/2)R; c_p = (5/2)R; γ = (5/3)R = circa 1,67.
se il gas è biatomico (esempio: ossigeno [O₂]):
c_v = (5/2)R; c_p = (7/2)R; γ = (7/5)R = circa 1,4.
se il gas è triatomico (esempio: anidride carbonica [CO₂]):
c_v = (7/2)R; c_p = (9/2)R; γ = (9/7)R = circa 1,29.